2012-12-10
Mathematical tools – Part 3
On
the morning of June 20, 1944, two weeks after D-Day, New York high
school students sitting for the Plane Geometry Regents exam were asked
to do the following construction: The
task posed almost 70 years ago was not difficult, but it also wasn’t
rote. It required the test-taker to make connections and to solve a
problem: to apply basic construction techniques to notions of similarity
and its theorems. Additionally, it required visualization skills:
before actually drawing the lines and arcs necessary to complete the
construction, students needed to envision the final picture.
The
task posed almost 70 years ago was not difficult, but it also wasn’t
rote. It required the test-taker to make connections and to solve a
problem: to apply basic construction techniques to notions of similarity
and its theorems. Additionally, it required visualization skills:
before actually drawing the lines and arcs necessary to complete the
construction, students needed to envision the final picture.
2012-11-27
Mathematical tools – Part 2
Were
it not for convoluted language, plenty of lawyers would be out of work.
Educators, though, shouldn't be subjected to such torture.
William McCallum, one of CCSSI’s authors, wrote in the comments section of an article appearing on The Atlantic Magazine website, written by Barry Garelick, ``I agree with you that there is a lot of misreading of the standards out there in the field, and this is a problem.’’ Such arrogance. The real problem is that CCSSI is poorly written, not only substantively, but also in its lack of clarity.
7.G.2’s ``Focus on constructing triangles from three measures of angles or sides...‘’ is at best, ambiguous. Writing intelligible English is not the same as constructing logic gates, where the definition of ``or’’ invariably includes the possibility of both. The parallelism in the sentence implies you are given either 3 angles or 3 sides, but we suspect it’s supposed to mean the following: ``Focus on constructing triangles given various combinations of three angles and/or sides.’’
William McCallum, one of CCSSI’s authors, wrote in the comments section of an article appearing on The Atlantic Magazine website, written by Barry Garelick, ``I agree with you that there is a lot of misreading of the standards out there in the field, and this is a problem.’’ Such arrogance. The real problem is that CCSSI is poorly written, not only substantively, but also in its lack of clarity.
7.G.2’s ``Focus on constructing triangles from three measures of angles or sides...‘’ is at best, ambiguous. Writing intelligible English is not the same as constructing logic gates, where the definition of ``or’’ invariably includes the possibility of both. The parallelism in the sentence implies you are given either 3 angles or 3 sides, but we suspect it’s supposed to mean the following: ``Focus on constructing triangles given various combinations of three angles and/or sides.’’
2012-11-12
Mathematical tools – Part 1
CCSSI 7.G.2 states, ``Draw
(freehand, with ruler and protractor, and with technology) geometric
shapes with given conditions. Focus on constructing triangles from three
measures of angles or sides, noticing when the conditions determine a
unique triangle, more than one triangle, or no triangle.’’
Some preliminaries before we parse this standard.
Protractors
We here at ccssimath.blogspot.com LOVE protractors. The way we see it, a (non-toxic, teething) protractor should be given to every newborn in their bassinet (thanks to Charles Schulz for the inspiration); perhaps the first one can be hanging from a mobile. A protractor (like a banjo) is a happy thing: it’s a smile, or a big letter D. A protractor is easy to hold, it’s too big to choke on, and it’s covered with numbers. It even has mystery and intrigue, for why would the numbers run in opposite directions? Rulers, in contrast, though useful, are dangerous things; they fit in the mouth and can be brandished as swords.
Some preliminaries before we parse this standard.
Protractors
We here at ccssimath.blogspot.com LOVE protractors. The way we see it, a (non-toxic, teething) protractor should be given to every newborn in their bassinet (thanks to Charles Schulz for the inspiration); perhaps the first one can be hanging from a mobile. A protractor (like a banjo) is a happy thing: it’s a smile, or a big letter D. A protractor is easy to hold, it’s too big to choke on, and it’s covered with numbers. It even has mystery and intrigue, for why would the numbers run in opposite directions? Rulers, in contrast, though useful, are dangerous things; they fit in the mouth and can be brandished as swords.
2012-10-12
Dodgy beginnings
In
legal argument, every assertion cites authority: when lawyers know they
are losing, they attempt to cloak weak arguments in language such as
``it is clear that’’, glossing over the insufficient basis for why;
strong assertions cite controlling authority, such as a prior ruling of
the U.S. Supreme Court. The same citation requirements hold true for
judicial opinions. The American common law system is grounded in its
constitutions and legislation, but also on the principle of stare decisis,
which means a strong legal opinion will cite another, preferably
higher, controlling authority for coming down on one side or another.
In the absence of binding authority, non-binding or persuasive
authority is relied on: someone made an argument that won a case in
another jurisdiction, the judge cites that decision and the law expands
to a new jurisdiction. Opponents of such decisions with weak legal
precedent may deride them as ``judicial activism’’, but judge-made law
is a fundamental component of how our system works, and indeed, how the
legal system has managed to survive. Of course, a judge may instead
reject another non-controlling decision and cite an alternative argument
for ruling differently. Thus, competing legal doctrines scatter like
leaves in the wind until a higher court decides to consolidate and
resolve contradictory rulings. It is often possible (and enlightening)
to trace a winning argument in a high court ruling down through various
lower court decisions and ultimately arrive at the original language
source, which can be the unprecedented argument of a jurist publishing
research (and personal opinions) in some obscure law journal. Thus
judge-made law, sometimes with questionable origins, becomes the law of the
land and not always for the better.
2012-08-29
Don't punt; take skills into the end zone
In 2011, the National Assessment of Educational Progress (otherwise known as ``The Nation’s Report Card’’) asked fourth graders to calculate the following:
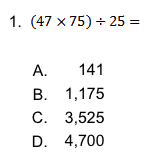


The results were 83%, 64% and 52% correct, respectively. Why was performance on the last task, arguably the easiest of the three, the worst? Answer: probably because it was the only one in which calculators were not allowed.
The results were 83%, 64% and 52% correct, respectively. Why was performance on the last task, arguably the easiest of the three, the worst? Answer: probably because it was the only one in which calculators were not allowed.
2012-07-26
Reaching higher? or grasping at straws?
In June 2010, the National Governors Association and the Council of Chief State School Officers, the two organizations that jointly produced CCSSI, issued Reaching Higher, a laudatory report co-signed by many influential people comprising ``The Common Core State Standards Validation Committee’’.
The report states, ``The NGA Center and CCSSO, as part of the CCSSI, convened a 25-member Validation Committee (VC) composed of leading figures in the education standards community. The committee was charged with providing independent, expert validation of the process of identifying the Common Core State Standards as part of the CCSSI.’’ (p.1)
The report states, ``The NGA Center and CCSSO, as part of the CCSSI, convened a 25-member Validation Committee (VC) composed of leading figures in the education standards community. The committee was charged with providing independent, expert validation of the process of identifying the Common Core State Standards as part of the CCSSI.’’ (p.1)
2012-07-10
Got subtraction?
A type of algebraic expression that befuddles legions of students is the following:
6x – (2x + 3)
6x – (2x + 3)
2012-06-26
The concept of area – Part 3
This is the third part of a multi-part blog post on the concept of area.
Pop quiz!
What’s the formula for the area of a triangle?
Pop quiz!
What’s the formula for the area of a triangle?
2012-06-15
The concept of area – Part 2
This is the second part of a multi-part blog post on the concept of area.
NAEP’s stark revelation of the extent to which students fail to understand the concept of area and lack basic problem solving skills warrants not a simple tweaking of current methodology, but a complete rethinking of how the topic of area is presented.
Existing mathematics curricula compartmentalize math skills into discrete chunks, the main benefits accruing to educators: it’s easier to teach and easier to write tests. The math bite approach to imparting skills is worse than the much-maligned notion of teaching to the test; it institutionalizes a testing regime, at the expense of developing students’ thinking skills. Even if they learn every standard, the parts remain disjointed without students gaining the real math wisdom that comes from synthesizing parts into a whole.
In earlier posts, we have tried to convey this notion of synthesis. We discussed our general philosophy: how applying concepts in useful ways abstracts the concept. We continue to advocate the concept → formal introduction → applications → abstraction sequence. Once concepts are synthesized, i.e., reach the abstract stage of understanding, actual thinking emerges and those concepts are ready to be applied in new, previously unencountered situations—and isn’t that the real point of education?
NAEP’s stark revelation of the extent to which students fail to understand the concept of area and lack basic problem solving skills warrants not a simple tweaking of current methodology, but a complete rethinking of how the topic of area is presented.
Existing mathematics curricula compartmentalize math skills into discrete chunks, the main benefits accruing to educators: it’s easier to teach and easier to write tests. The math bite approach to imparting skills is worse than the much-maligned notion of teaching to the test; it institutionalizes a testing regime, at the expense of developing students’ thinking skills. Even if they learn every standard, the parts remain disjointed without students gaining the real math wisdom that comes from synthesizing parts into a whole.
In earlier posts, we have tried to convey this notion of synthesis. We discussed our general philosophy: how applying concepts in useful ways abstracts the concept. We continue to advocate the concept → formal introduction → applications → abstraction sequence. Once concepts are synthesized, i.e., reach the abstract stage of understanding, actual thinking emerges and those concepts are ready to be applied in new, previously unencountered situations—and isn’t that the real point of education?
2012-06-05
The concept of area – Part 1
This is Part 1 of a multi-part blog post on the concept of area.
In 2005, the National Assessment of Educational Progress, otherwise known as ``The Nation's Report Card'', presented the following question:
 This
question was given to fourth graders, 47% of whom answered correctly.
This result would have been mediocre if tiling had been taught by fourth
grade and good if tiling had not been taught (i.e., students
were able to figure it out on their own)—but we don’t know which.
This
question was given to fourth graders, 47% of whom answered correctly.
This result would have been mediocre if tiling had been taught by fourth
grade and good if tiling had not been taught (i.e., students
were able to figure it out on their own)—but we don’t know which.
In 2005, the National Assessment of Educational Progress, otherwise known as ``The Nation's Report Card'', presented the following question:
2012-05-29
Wholesale whole-number murder and redemption
An extended mathematics metaphor:
Flowing under the pre-K through high school curriculum, like the ever-widening Mississippi, is a steady expansion of the number system and its corresponding basic operations.
Important milepost concepts and mathematical problems which are posed, deconstructed and solved throughout those years are like the flatboats and steamboats of Mark Twain's era which floated upon the Mississippi's waters.
One doesn't seek to control the river, because the number system and its operations exist in nature, but we can select what floats on it and where to travel. Choosing when and how to introduce concepts, what problems to pose, and where they fit is the foremost responsibility of a standards and curriculum developer.
Flowing under the pre-K through high school curriculum, like the ever-widening Mississippi, is a steady expansion of the number system and its corresponding basic operations.
Important milepost concepts and mathematical problems which are posed, deconstructed and solved throughout those years are like the flatboats and steamboats of Mark Twain's era which floated upon the Mississippi's waters.
One doesn't seek to control the river, because the number system and its operations exist in nature, but we can select what floats on it and where to travel. Choosing when and how to introduce concepts, what problems to pose, and where they fit is the foremost responsibility of a standards and curriculum developer.
2012-05-18
About the bloggers…
First, a pledge:
We should interpose that we are not salaried educators, we are not political ideologues, we have no personal vendettas, we are not self-absorbed egoists, we have no children in school, and we have no pecuniary interest in the future success or failure of various educational reform efforts. We are disinterested parties, and we are not selling any product or service. We own no stock in any education-related publicly traded company. (Did we overlook anything?)
Because we are unbeholden and free of conflicts of interest, we are able to speak truth to educrat-power.
We, the bloggers, hereby affirm that we have a particular interest in improving K-12 mathematics education and will do what little we can to advance that worthy cause in the confines of this blog.Since it is impossible to expound on all that is right and wrong with Common Core in one fell swoop, we can only address issues piecemeal, at the risk of occasionally sounding incoherent, or even worse, looking like bloviating ignorami. We know that we may contradict ourselves at times. Writing a blog is difficult; kudos to you bloggers out there.
We should interpose that we are not salaried educators, we are not political ideologues, we have no personal vendettas, we are not self-absorbed egoists, we have no children in school, and we have no pecuniary interest in the future success or failure of various educational reform efforts. We are disinterested parties, and we are not selling any product or service. We own no stock in any education-related publicly traded company. (Did we overlook anything?)
Because we are unbeholden and free of conflicts of interest, we are able to speak truth to educrat-power.
[It is remotely possible that someone will want
to hire us in some capacity to spiel on their (more heavily trafficked) website,
so some of the previous statements may have to be superseded. In the unlikely event that
happens, we'll be sure to let readers know. We believe in full
disclosure about any financial or other potential biases.]
We
have what we consider to be sufficient credentials to comment on the matter
(and we'll let readers judge that statement based on the content of our posts), but we remain anonymous to let our words
speak, rather than potentially being directly assailed or having our
credibility questioned. We wish to draw attention to the issues, not to ourselves.
2012-05-17
Common Core: a national cop-out, not a national curriculum
A cautionary tale...
In the 1980’s, the combination of banking deregulation and lack of oversight allowed a breed of banks known as Savings & Loans to embark on a scheme of making risky loans using depositor funds. If the loans worked out, the S&L’s stood to profit, but if the loans failed, the deposits were insured by a federal insurance company (the FSLIC). For the S&L’s, it was a ``heads I win, tails you (the insurance company) lose'' situation.
***
In the 1980’s, the combination of banking deregulation and lack of oversight allowed a breed of banks known as Savings & Loans to embark on a scheme of making risky loans using depositor funds. If the loans worked out, the S&L’s stood to profit, but if the loans failed, the deposits were insured by a federal insurance company (the FSLIC). For the S&L’s, it was a ``heads I win, tails you (the insurance company) lose'' situation.
But it was
even worse than that.
When enough
loans went bad (of course they did, otherwise it wouldn't be a story), the
FSLIC was depleted and went bankrupt, taxpayers footed the $100 billion bill, and (although
we are not presenting the entire history lesson) these
events contributed to an economic meltdown that is commonly known as the
``S&L crisis''.
What can we
learn from history? For us, it is when someone hands you a ``heads I win,
tails you lose'' proposition, be very, very careful before signing on the
dotted line.
***
2012-05-08
Counting and its applications
Counting, notwithstanding the, er, tale of Clever Hans, is so basic that it seems to be an innate ability in several animal species, according to an article published in Scientific American™ in September 2009.
[Clarification: the word ``basic'' above is being used in context as ``fundamental'', not ``simple''. See tweet below linking to this blog post that missed the point.]
Parents teach their youngsters to count to 10, or children learn it on Sesame Street, and there are numerous studies showing babies can conceive of small numbers and preschoolers can judge greater or less than without knowing exact numbers, but by understanding approximate counts.
In mathematical parlance, the counting numbers are also called the ``natural'' numbers, as existing in nature.
So how is it possible to teach counting, the most natural of mathematical skills, unnaturally? The worst way is to force memorization of numbers and number names before the concept is understood. What kindergartner do you know that owns 90 of anything, except maybe for Beanie Babies? Open a Scrabble set and look at the 100 tiles. Is that a number of objects that a kindergartner needs to comprehend in their child's world? Memorizing the names of numbers at the age of 5 before actually understanding the concept of the number is simply put, backwards. Mathematics should not be taught that way. A child should understand the number along with the name, before reading, and then writing the number.
If particularly anal parents want to push too-large numbers on their child at an early age for fear of falling behind, so be it, but the paranoia should not be systemic.
CCSSI standard K.CC.1 ``Count to 100...’’ carries into the next year's standard 1.NBT.1 ``Count to 120...’’ along with a few variations on the theme. We won’t pause long to chide CCSSI for such arbitrary parameters because there is a much more compelling standard in the parallel Measurement and Data strand that pertains to counting, which creates the potential for some real advancement of thinking and analytical skills in early childhood.
[Clarification: the word ``basic'' above is being used in context as ``fundamental'', not ``simple''. See tweet below linking to this blog post that missed the point.]
Parents teach their youngsters to count to 10, or children learn it on Sesame Street, and there are numerous studies showing babies can conceive of small numbers and preschoolers can judge greater or less than without knowing exact numbers, but by understanding approximate counts.
In mathematical parlance, the counting numbers are also called the ``natural'' numbers, as existing in nature.
So how is it possible to teach counting, the most natural of mathematical skills, unnaturally? The worst way is to force memorization of numbers and number names before the concept is understood. What kindergartner do you know that owns 90 of anything, except maybe for Beanie Babies? Open a Scrabble set and look at the 100 tiles. Is that a number of objects that a kindergartner needs to comprehend in their child's world? Memorizing the names of numbers at the age of 5 before actually understanding the concept of the number is simply put, backwards. Mathematics should not be taught that way. A child should understand the number along with the name, before reading, and then writing the number.
If particularly anal parents want to push too-large numbers on their child at an early age for fear of falling behind, so be it, but the paranoia should not be systemic.
CCSSI standard K.CC.1 ``Count to 100...’’ carries into the next year's standard 1.NBT.1 ``Count to 120...’’ along with a few variations on the theme. We won’t pause long to chide CCSSI for such arbitrary parameters because there is a much more compelling standard in the parallel Measurement and Data strand that pertains to counting, which creates the potential for some real advancement of thinking and analytical skills in early childhood.
2012-04-30
How many is a billion?
In 1992, the National Assessment of Educational Progress, otherwise known as ``The Nation's Report Card'', presented the following question:

In this five option multiple-choice question, 22% of American eighth graders got the correct answer. We could analyze in purely statistical terms how much better than wild guessing this is, but it's clearly not much. In other words, the results essentially meant that the entire nation's soon-to-enter high school students did not understand the difference between a million and a billion.

In this five option multiple-choice question, 22% of American eighth graders got the correct answer. We could analyze in purely statistical terms how much better than wild guessing this is, but it's clearly not much. In other words, the results essentially meant that the entire nation's soon-to-enter high school students did not understand the difference between a million and a billion.
2012-04-26
Decomposing numbers in kindergarten
Common Core standard K.OA.3 states, ``Decompose numbers less than or equal to
10 into pairs in more than one way, e.g., by using objects or drawings,
and record each decomposition by a drawing or equation (e.g., 5 = 2 + 3
and 5 = 4 + 1).''
Although it falls under the general heading of addition and subtraction, the mathematical concept that this exercise is supposed to teach kindergartners is mystifying. By ``pairs'', does it really mean ``groups''? Is it an introduction to odd and even numbers? The commutative property? Transitivity? Algebra? Combinatorics? Or to impress on the kindergartner that both 4 + 1 and 2 + 3 equal 5?
Although it falls under the general heading of addition and subtraction, the mathematical concept that this exercise is supposed to teach kindergartners is mystifying. By ``pairs'', does it really mean ``groups''? Is it an introduction to odd and even numbers? The commutative property? Transitivity? Algebra? Combinatorics? Or to impress on the kindergartner that both 4 + 1 and 2 + 3 equal 5?
2012-04-24
Addition and subtraction ad nauseam
The pre-CCSSI 2008 Final Report of the National Mathematics Advisory Panel, commissioned by the U.S. Department of Education, in a section entitled ``A Need for Coherence'', was bluntly critical of
``...U.S. curricula [that] generally review and extend at successive grade levels many (if not most) topics already presented at earlier grade levels, while the top-performing countries are more likely to expect closure after exposure, development, and refinement of a particular topic. These critical differences distinguish a spiral curriculum (common in many subjects in U.S. curricula) from one built on developing proficiency—a curriculum that expects proficiency in the topics that are presented before more complex or difficult topics are introduced.''Every math teacher knows the concept of spiraling, the revisiting of old problems to ``reinforce'' concepts lest students should forget. The NMAP in no uncertain terms clearly rejected this approach, but what does Common Core do? It introduces addition and subtraction in kindergarten, ``students should see addition and subtraction equations,'' yet CCSSI is still covering addition and subtraction of whole numbers into the fourth grade:
2012-04-23
Not a diatribe
This is not a blog written by those who oppose a national curriculum on the basis of an anti-government ideology. A common standard makes sense. The highest performing countries have them. The problem arises when you commit an entire nation to a substandard, untested curriculum. This blog reflects our singular commitment to a better mathematics education for all.
The concept of none
Common Core's first major blunder is its treatment of nothing.
From CCSSI K.CC.3: ``Write numbers from 0 to 20. Represent a number of objects with a
written numeral 0-20 (with 0 representing a count of no objects).''
Long before children read and write, they speak, and long before they write numbers, they count and conceptualize. As young children, we don't count starting at zero, we start at one.
At what age can a child abstract that when you take away everything, you have nothing and that is represented by the number zero? Obviously, it's a concept you introduce in stages: everyone knows ``none'' or ``nothing'' before you abstract to the number 0. We don't claim to know what the appropriate age is, but we KNOW this doesn't belong in kindergarten, before counting is mastered. We'd guess that by the end of first grade, after learning about ``taking away'' and subtraction, every child should understand both the concept and perhaps the number. But the steps have to be clearly set out as part of the curriculum; otherwise, ``0'' will likely be glossed over by teachers in the classroom as something trivial and obvious, which it is not.
CCSSI's ``Mathematical practice No. 2'' is: ``Reason abstractly and quantitatively.'' The concept of none is the first major abstract idea in mathematics, and it needs careful treatment.
[CCSSI does in fact mention the sequence from concept of none to digit 0...in the Mathematical Standards for High School, p. 58. Which elementary teachers are reading the high school standards?]
From CCSSI K.CC.3: ``Write numbers from 0 to 20. Represent a number of objects with a
written numeral 0-20 (with 0 representing a count of no objects).''
Long before children read and write, they speak, and long before they write numbers, they count and conceptualize. As young children, we don't count starting at zero, we start at one.
At what age can a child abstract that when you take away everything, you have nothing and that is represented by the number zero? Obviously, it's a concept you introduce in stages: everyone knows ``none'' or ``nothing'' before you abstract to the number 0. We don't claim to know what the appropriate age is, but we KNOW this doesn't belong in kindergarten, before counting is mastered. We'd guess that by the end of first grade, after learning about ``taking away'' and subtraction, every child should understand both the concept and perhaps the number. But the steps have to be clearly set out as part of the curriculum; otherwise, ``0'' will likely be glossed over by teachers in the classroom as something trivial and obvious, which it is not.
CCSSI's ``Mathematical practice No. 2'' is: ``Reason abstractly and quantitatively.'' The concept of none is the first major abstract idea in mathematics, and it needs careful treatment.
[CCSSI does in fact mention the sequence from concept of none to digit 0...in the Mathematical Standards for High School, p. 58. Which elementary teachers are reading the high school standards?]
Does a kindergartner need to know what a hexagon is?
From CCSSI: Kindergartners ``identify, name, and describe basic two-dimensional shapes, such as squares, triangles, circles, rectangles, and hexagons...''
Can every kindergartner visually distinguish between a square and a rectangle? Likely. Two dimensions and three dimensions? Dubious. And know what a hexagon is? No, it's age inappropriate. What's the point of pushing a kindergartner to know what a hexagon is? Is this going to lay the foundation to be college ready?
From CCSSI, a question that a teacher should ask a kindergartner and they are expected to understand and complete the task: “Can you join these two triangles with full sides touching to make a rectangle?”
``with full sides touching''? It sounds awkward because it is awkward.
Shouldn't a kindergartner be playing with blocks instead? Any kindergartner playing with blocks knows there are rectangular blocks and triangular blocks. If you put two triangular blocks one on top of the other, the top block will slide off. Why make this a goal-oriented and evaluated task?
Leave it to CCSSI to take the fun out of blocks.
Can every kindergartner visually distinguish between a square and a rectangle? Likely. Two dimensions and three dimensions? Dubious. And know what a hexagon is? No, it's age inappropriate. What's the point of pushing a kindergartner to know what a hexagon is? Is this going to lay the foundation to be college ready?
From CCSSI, a question that a teacher should ask a kindergartner and they are expected to understand and complete the task: “Can you join these two triangles with full sides touching to make a rectangle?”
``with full sides touching''? It sounds awkward because it is awkward.
Shouldn't a kindergartner be playing with blocks instead? Any kindergartner playing with blocks knows there are rectangular blocks and triangular blocks. If you put two triangular blocks one on top of the other, the top block will slide off. Why make this a goal-oriented and evaluated task?
Leave it to CCSSI to take the fun out of blocks.
2012-04-20
Common Core's lack of humility
If nothing else, the statements in and around the standards are self-serving and self-aggrandizing. Why is this necessary? Let the standards speak for themselves.
To wit:
``The standards...are clear, understandable and consistent.''
``To deliver on the promise of common standards, the standards must address the problem of a curriculum that is 'a mile wide and an inch deep.' These Standards are a substantial answer to that challenge.'' (emphasis added)
``What is important to keep in mind is that the progression in the Common Core State Standards is mathematically coherent and leads to college and career readiness at an internationally competitive level.''
Oh, really? No one knows what the outcome of CCSSI will be. Fast forward 12 years for a reality check when the first students graduate high school who had a lifetime of Common Core, and the people who made these highfalutin claims are already collecting their pensions.
To wit:
``The standards...are clear, understandable and consistent.''
``To deliver on the promise of common standards, the standards must address the problem of a curriculum that is 'a mile wide and an inch deep.' These Standards are a substantial answer to that challenge.'' (emphasis added)
``What is important to keep in mind is that the progression in the Common Core State Standards is mathematically coherent and leads to college and career readiness at an internationally competitive level.''
Oh, really? No one knows what the outcome of CCSSI will be. Fast forward 12 years for a reality check when the first students graduate high school who had a lifetime of Common Core, and the people who made these highfalutin claims are already collecting their pensions.
CCSSI coming soon to a school near you
The Common Core State Standards Initiative has been adopted and is being implemented by over 40 states and DC. This blog is taking a closer look at the math standards, and math teaching in general. A list of blog entries is at the right.
Subscribe to:
Posts (Atom)


